一、逻辑代数中的三种基本运算
逻辑代数中有三种基本运算,分别是 与(AND)、或(OR)、非(NOT)
- 与 运算记作 Y=A·B ,全 1 为 1,否则为0。
- 或 运算记作 Y=A+B ,有 1 为 1,全 0 为 0。
- 非 运算记作 Y=A'(有些地方也写作A上面加一个横杠 或 ~A等),取反即可。
他们官方认定的逻辑运算图形符号由以下两套。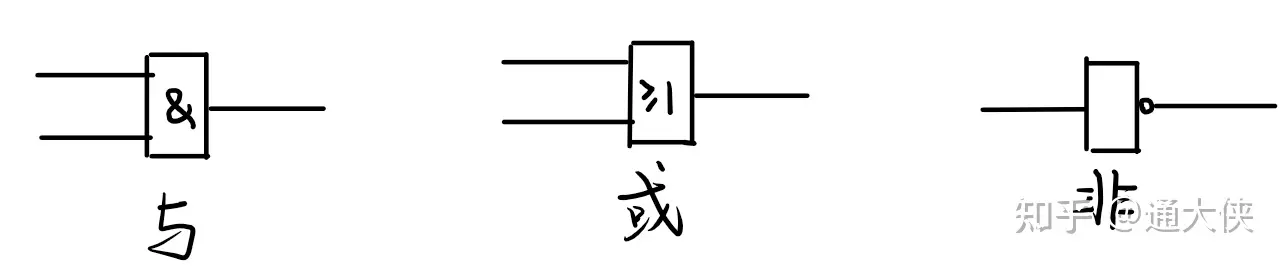

二、更复杂的逻辑运算
更复杂的逻辑运算都可以用与、或、非的组合来实现,例如:与非(nand)、或非(nor)、与或非(and-nor)、异或(xor)、同或(xnor)等。下面解释一些常见的逻辑运算符号:
- 与非 运算,全1为0,否则为1.(对与运算取反)
- 或非 运算,全0为1,否则为0.(对或运算取反)
- 异或 运算,不同为1,相同为0.
- 同或 运算,相同为1,不同为0.
他们的图像表达为: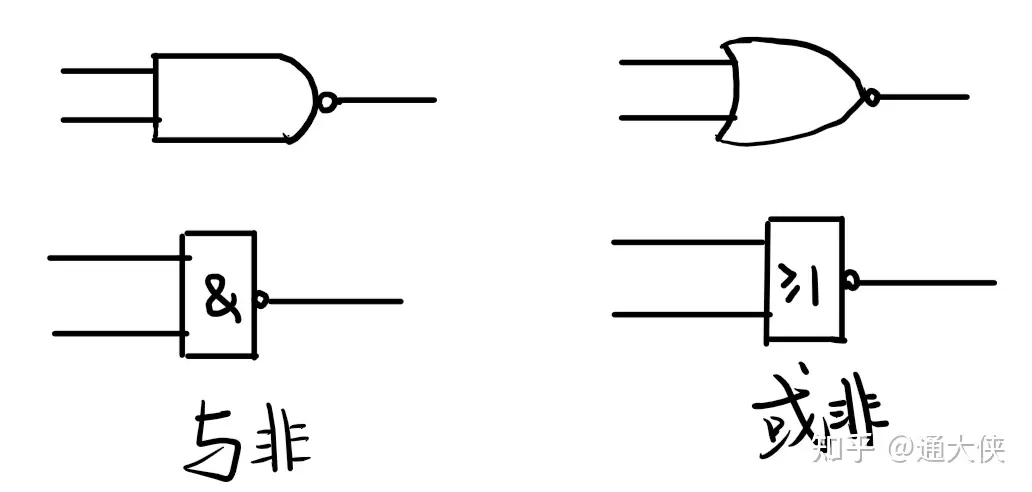
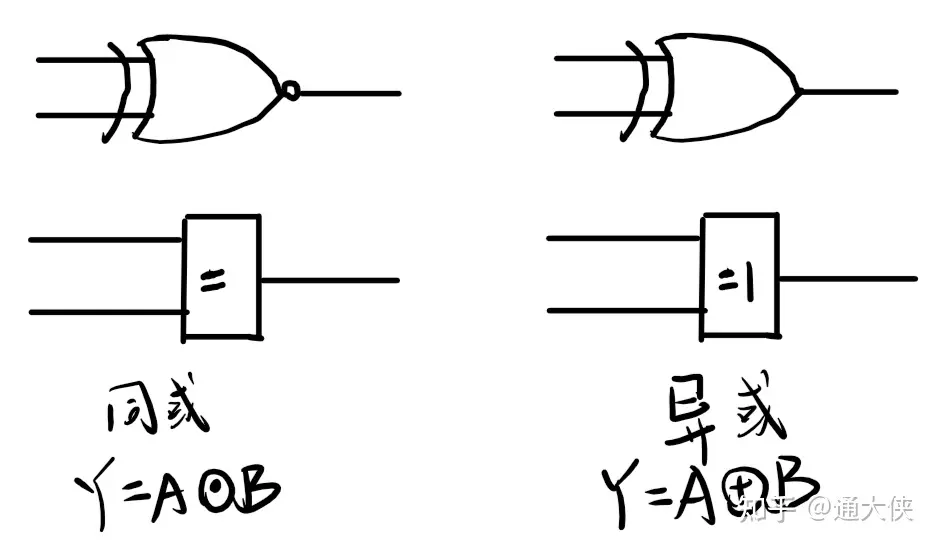
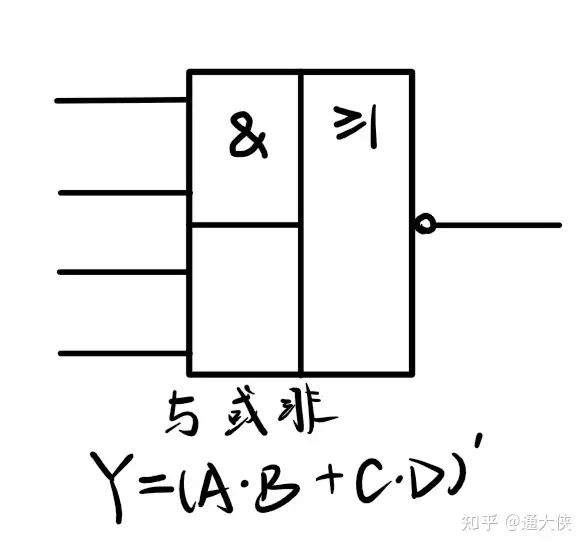
三、逻辑代数的基本公式:
逻辑代数满足交换律、结合律、分配律、反演律、还原律。
- 交换律:A·B=B·A,A+B=B+A
- 结合律:A·(B·C)=(A·B)·C,A+(B+C)=(A+B)+C
- 分配律:A·(B+C)=A·B+A·C,A+(B·C)=(A+B)·(A+C)
- 反演律:(A·B)'=A'+B',(A+B)'=A'+B'
- 还原律:(A')'=A
评论0
暂时没有评论